sábado, 20 de marzo de 2010

Filtro comb

Roberto Jesus Rojas
CI:14908981
Asignatura:CAF
Fuente: Wikipedia.
En el procesamiento de señales, un filtro comb (o peine) se produce al sumarle a la señal original una versión retrasada en el tiempo de sí misma, causando así interferencia constructiva y destructiva. La respuesta en frecuencia de un filtro comb consiste en una serie de picos regularmente espaciados, cuya figura se asemeja a la de un peine (comb, en inglés).
Los filtros comb se pueden identificar de acuerdo al tipo de señal sumada a la entrante. Si sólo depende de los valores previos en la entrada se denomina feedforward o filtro FIR (de Finite Impulse Response: respuesta a impulso finita), y si depende sólo de los valores previos de la salida se llama feedback o filtro IIR (respuesta a impulso infinita). Se pueden implementar en un dominio temporal discreto o contínuo; este artículo se basará en implementaciones en tiempo discreto; las propiedades de los filtros en el dominio temporal contínuo son muy similares

Diagrama y análisis espectral de un filtro comb (IIR+FIR) aplicado a ruido blanco.
.

Filtros FIR o Feedforward

La estructura general de un filtro comb feedforward es mostrada a la derecha, y es descripta por la siguiente ecuación recurrente:
\ y[n] = x[n] + \alpha x[n-K]
donde K es el tamaño del retraso (medido en muestras), y α es un factor de escalamiento aplicado a la señal retrasada. Si tomamos la transformada Z en ambos lados de la ecuación, obtenemos:
\ Y(z) = (1 + \alpha z^{-K}) X(z)
Podemos entonces definir la función de transferencia de la siguiente manera:
\ H(z) = \frac{Y(z)}{X(z)} = 1 + \alpha z^{-K} = \frac{z^K + \alpha}{z^K}

Estructura de un filtro comb FIR o Feedforward.

Respuesta en magnitud de un filtro comb Feedforward para distintos valores positivos de α.

Respuesta en magnitud de un filtro Feedforward para distintos valores negativos de α.
Gnome-speakernotes.svg
Ruido blanco sin filtrar
¡Precaución en todos los audios! Se sugiere escuchar a un nivel bajo de volumen para evitar daños auditivos y en el sistema de amplificación

Ruido blanco filtrado con un filtro comb FIR con un retraso de 3 milisegundos, y un coeficiente α = 1

Ruido blanco filtrado con un filtro comb FIR con un retraso de 3 milisegundos, y un coeficiente α = 0,75
Archivo:Filtro comb FIR con alfa=0 75.ogg

Ruido blanco filtrado con un filtro comb FIR con un retraso de 3 milisegundos, y un coeficiente α = 0,5

Ruido blanco filtrado con un filtro comb IIR con un retraso de 3 milisegundos, y un coeficiente α = 0,9

Ruido blanco filtrado con un filtro comb IIR con un retraso de 3 milisegundos, y un coeficiente α = 0,75
Archivo:Filtro comb IIR con alfa=0 75.ogg

Ruido blanco filtrado con un filtro comb IIR con un retraso de 3 milisegundos, y un coeficiente α = 0,5

¿Problemas al escuchar estos archivos? Vea Ayuda:Multimedia.

Respuesta en frecuencia [editar]

Para obtener la respuesta en frecuencia de un sistema temporalmente discreto expresado en el dominio complejo Z, hacemos la sustitución z = ejω. Para nuestro filtro comb FIR tenemos:
\ H(e^{j \omega}) = 1 + \alpha e^{-j \omega K}
Uno de los parámetros de interés es su respuesta en magnitud, ignorando la fase. Ésta queda definida como:
\ | H(e^{j \omega}) | = \sqrt{\Re\{H(e^{j \omega})\}^2 + \Im\{H(e^{j \omega})\}^2}
En el caso de un filtro FIR es:
\ | H(e^{j \omega}) | = \sqrt{(1 + \alpha^2) + 2 \alpha \cos(\omega K)}
Nótese que el término (1 + α2) es constante, con lo que el término 2αcos(ωK) varía periódicamente. Por lo tanto la respuesta en magnitud de un filtro FIR es periódica.
Los gráficos a la derecha muestran la respuesta en magnitud para varios valores de α, demostrando esta periodicidad. Algunas propiedades importantes:
  • La respuesta periódicamente decae hasta un mínimo local (conocido a veces como notch), y luego crece hasta un máximo local (también conocido como peak).
  • Los niveles máximos y mínimos están siempre equidistantes de 1.
  • Cuando \alpha = \pm 1, el mínimo tiene amplitud 0. En este caso el mínimo es conocido como cero.
  • El máximo de los valores positivos de α coincide con el mínimo de los valores negativos de α, y viceversa.

Interpretación de polos y ceros [editar]

Mirando nuevamente a la función de transferencia en el dominio complejo Z de un filtro comb FIR:
\ H(z) = \frac{z^K + \alpha}{z^K}
vemos que el numerador es igual a cero cuando zK = − α. Tiene por tanto K soluciones, que graficadas se encuentran igualmente espaciadas alrededor de un círculo en el plano complejo; esos son los ceros de la función de transferencia. El denominador es cero cuando zK = 0, dando K polos en z = 0. El gráfico correspondiente se ve abajo.

Gráfico de polos y ceros de un filtro comb FIR con K = 8 y α = 0.5.

Gráfico de polos y ceros de un filtro comb FIR con K = 8 y α = − 0.5.

Filtros IIR o Feedback [editar]


Estructura de un filtro comb IIR o feedback.

Respuesta en magnitud de un filtro comb feedback para distintos valores positivos de α.

Respuesta en magnitud de un filtro comb feedback para distintos valores negativos de α.
En forma similar, la estructura general de un filtro comb IIR es mostrada a la derecha, y es descripta por la siguiente ecuación recurrente:
\ y[n] = x[n] + \alpha y[n-K]
Si reacomodamos la ecuación para que todos los términos en y estén del lado izquierdo y tomamos la transformada Z, tenemos:
\ (1 - \alpha z^{-K}) Y(z) = X(z)
La función de transferencia es, por lo tanto:
\ H(z) = \frac{Y(z)}{X(z)} = \frac{1}{1 - \alpha z^{-K}} = \frac{z^K}{z^K - \alpha}

Respuesta en frecuencia [editar]

Si hacemos la sustitución z = ejω en el dominio complejo Z, obtenemos la siguiente expresión para los filtros comb IIR:
\ H(e^{j \omega}) = \frac{1}{1 - \alpha e^{-j \omega K}}
La respuesta en magnitud se calcula entonces:
\ | H(e^{j \omega}) | = \frac{1}{\sqrt{(1 + \alpha^2) - 2 \alpha \cos(\omega K)}}
Nuevamente, la respuesta es periódica, como demuestra el gráfico a la derecha. El filtro comb IIR tiene algunas propiedades en común con los FIR:
  • La respuesta periódicamente decae hasta un mínimo local y crece hasta un máximo local.
  • El máximo de los valores positivos de α coincide con el mínimo de los valores negativos de α, y viceversa.
De cualquier manera existen diferencias importantes, debido a que la respuesta en magnitud depende de un término ubicado en el denominador:
  • Los niveles de los máximos y mínimos no son equidistantes de 1.
  • El filtro es estable sólo si | α | es menor que 1. Como podemos ver en los gráficos, cuando | α | crece, las amplitudes de los picos máximos suben rápidamente.

Interpretación de polos y ceros [editar]

Mirando nuevamente la función de transferencia en el dominio Z de un filtro comb IIR:
\ H(z) = \frac{z^K}{z^K - \alpha}
Esta vez, el numerador es cero siempre que zK = 0, dando K ceros cuando z = 0. El denominador es igual a cero cuando zK = α. Esto tiene K soluciones posibles, igualmente espaciadas alrededor de un círculo ubicado en el plano complejo; esos son los polos de la función de transferencia. Esto produce un gráfico como el que se muestra a continuación.

Gráfico de polos y ceros de un filtro comb IIR con K = 8 y α = 0.5.

Gráfico de polos y ceros de un filtro comb IIR con K = 8 y α = − 0.5.

Filtros comb en el tiempo continuo [editar]

Los filtros comb pueden ser implementados también en el tiempo continuo. Los FIR son descriptos por la siguiente ecuación:
\ y(t) = x(t) + \alpha x(t - \tau)
y los IIR:
\ y(t) = x(t) + \alpha y(t - \tau)
donde τ es el retraso de la señal (medido en segundos).
Utilizando la Transformada de Laplace se puede calcular la respuesta en frecuencia a partir de la función de transferencia, en forma similar al caso discreto con la Transformada Z. Las respuestas de los filtros expresados arriba para tiempo continuo entonces quedan, respectivamente:
\ H(\omega) = 1 + \alpha e^{-j \omega \tau}
\ H(\omega) = \frac{1}{1 - \alpha e^{-j \omega \tau}}
Las implementaciones en el tiempo contínuo comparten todas las propiedades de las respectivas implementaciones en el tiempo discreto.

Aplicaciones

Los filtros comb son utilizados en una variedad de aplicaciones de procesamiento de señales. Algunas de ellas son:

Publicado por en
Etiquetas:

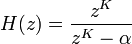
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)